Binary Search Tree: Implementation in C++

Binary Search Tree:

Before going ahead: I hope you've read all that is required about trees. If you haven't you can read it here: https://rishabhjainiitbhu.blogspot.com/2019/07/introduction-to-trees-c-data-structures.html
Further reading, basics about Binary trees is also suggested, you can do it here:
https://rishabhjainiitbhu.blogspot.com/2019/07/binary-trees-c-trees.html


Binary Search Trees(BSTs) are balanced binary trees, such that for each node in the tree value of all the nodes in the left subtree are smaller or equal than the parent node, and the value of all the nodes in the right subtree are larger than the parent node.

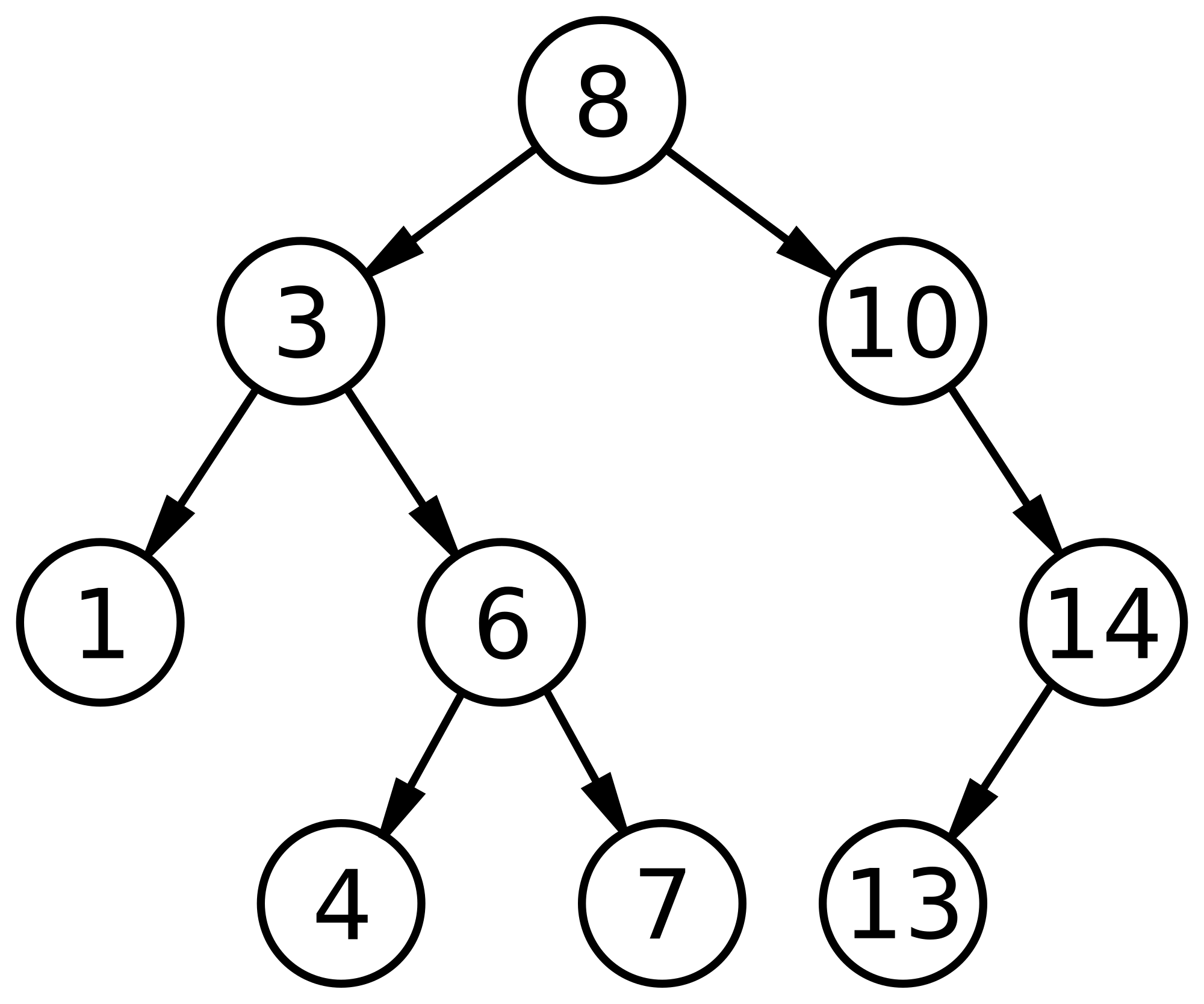
Thus the above-given graph is a binary search tree.

Binary search tree lets you do search, Insertion, and removal of all elements in order of $O(log n)$

Here is the code for insertion and searching in a BST.

The Code:

Here is the code for representing each node. We have used structures to represent it.

	struct Node{
	int data;
	Node* left;
	Node* right;
	};

Each Node contains a link to a right and a left sub-tree besides the data field.

Here is the class BST

class BST{
	private:
	Node* root;
	public:
	BST(){
	root = NULL;
	}
	void add(int data, Node** n){
	Node* parent = *n;
	if(parent == NULL){
	Node* new_node = new Node;
	new_node->data = data;
	*n = new_node;
	return;
	}
	if(parent->data>data){
	add(data, &(parent->left));
	}else{
	add(data, &(parent->right));
	}
	}
	bool search(int data, Node** n){
	Node* parent = *n;
	if(parent == NULL){
	return false;
	}
	if(parent->data == data)
	return true;
	if(data > parent->data){
	return search(data, &(parent->right));
	}else{
	return search(data, &(parent->left));
	}
	}
	Node* getRoot(){
	return root;
	}
	};

Let us break it piece by piece. Here is the insertion function:

void add(int data, Node** n){
	Node* parent = *n;
	if(parent == NULL){
	Node* new_node = new Node;
	new_node->data = data;
	*n = new_node;
	return;
	}
	if(parent->data>data){
	add(data, &(parent->left));
	}else{
	add(data, &(parent->right));
	}
	}

We pass have used recurrsion to add the data. At each node we check if the node is null, in that case we assign it a new node. If not, we check if the given data is greater than the data in the node and proceed accordingly. The process of insertion takes $O(log n)$

Note here, we have used double pointers to pass the root node by reference.

Here is the search function:

bool search(int data, Node** n){
	Node* parent = *n;
	if(parent == NULL){
	return false;
	}
	if(parent->data == data)
	return true;
	if(data > parent->data){
	return search(data, &(parent->right));
	}else{
	return search(data, &(parent->left));
	}
	}

The code is simple if you've got the process of insertion. Again we have used recursion to search elements and it takes $O(log n)$ to search elements.