Forward Propagation:
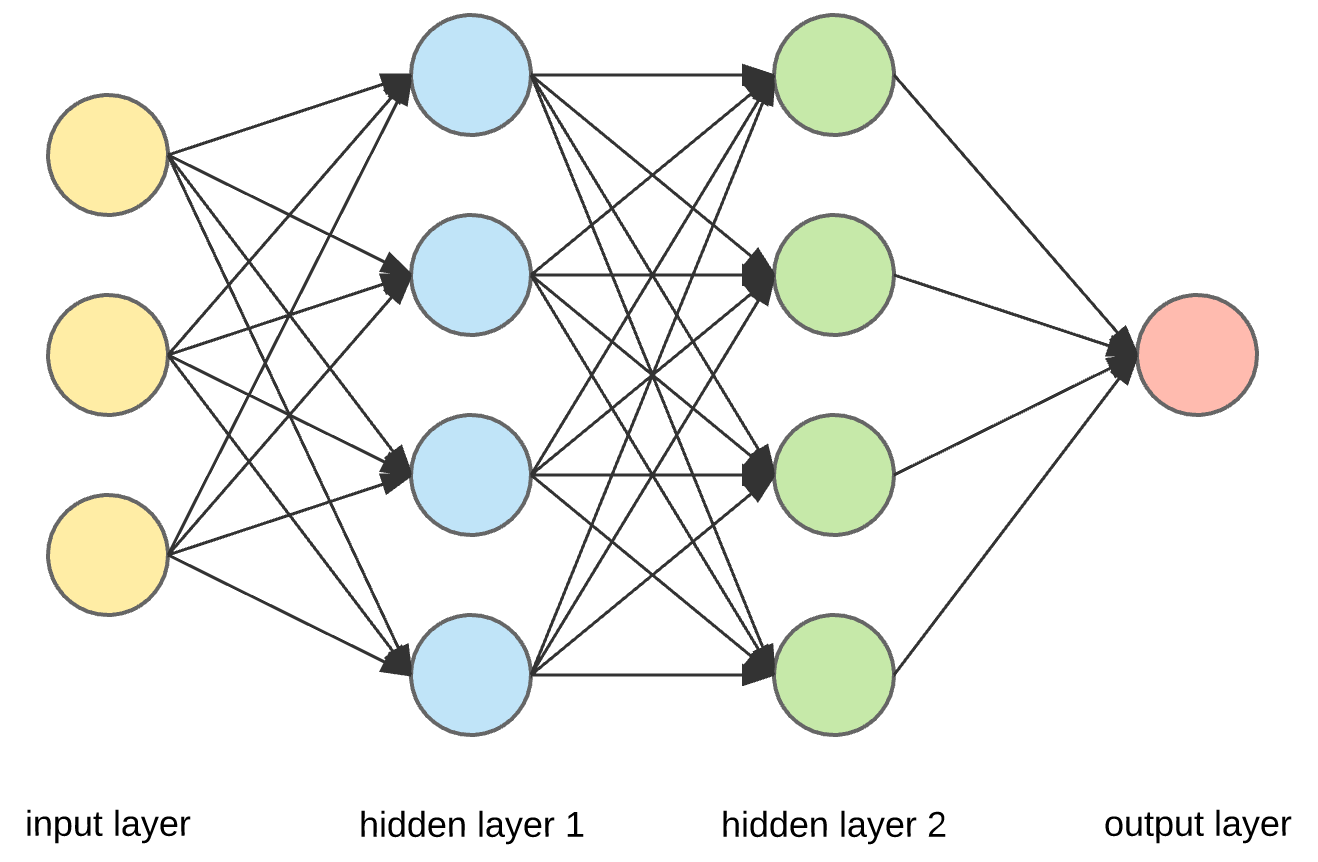
Recall that \[ a(2)(1) = g(theta1(1)(0)*x0 + theta1(1)(1)*x1 + theta1(1)(2)* x2)\],
\[a(2)(2) = g(theta1(2)(0)x0 + theta1(2)(1)x1 + theta1(2)(2)x2)\],
\[a(2)(3) = g(theta1(3)(0)x0 + theta1(3)(1)x1 + theta1(3)(2)x2)\], so on and so forth.
We can vectorize the complete mathematics that neural network does, and it will look better than, then it seems now.
if theta1 is a matrix of dimensions 4*3, and x is a vector of size (3, 1), the activation of each unit in the second layer can be evaluated as follows:
\[a2 = g(theta1@x)\].
Note that we are not counting bias term here, if you want you can add it, you'll only need to add one to each activation vector at each step and @ is the operator for matrix multiplication in python.
Now, similarly the activations in the third layer can be evaluated as follows:
\[a3 = g(theta2@a2)\]
And finally the output can be calculated as:
\[h(x) = g(theta3@a3)\].
This was all about predicting, given thetas how to predict the output for a set of features. In an upcoming post, we'll learn how to train Neural Network to learn the thetas.
We can vectorize the complete mathematics that neural network does, and it will look better than, then it seems now.
if theta1 is a matrix of dimensions 4*3, and x is a vector of size (3, 1), the activation of each unit in the second layer can be evaluated as follows:
\[a2 = g(theta1@x)\].
Note that we are not counting bias term here, if you want you can add it, you'll only need to add one to each activation vector at each step and @ is the operator for matrix multiplication in python.
Now, similarly the activations in the third layer can be evaluated as follows:
\[a3 = g(theta2@a2)\]
And finally the output can be calculated as:
\[h(x) = g(theta3@a3)\].
This was all about predicting, given thetas how to predict the output for a set of features. In an upcoming post, we'll learn how to train Neural Network to learn the thetas.
No comments:
Post a Comment